What is meant by the term "rolling cadence"?

[rstreet (Rachel Street)]

While considering trade-offs between different survey strategies, consideration is being given to the pros and cons of a rolling cadence. However, different people seemed to have different concepts of exactly what this referred to, so I posed the question to @fed and @MelissaGraham.

This thread records our conclusions, but I invite responses from @ljones, @yoachim, @tribeiro and the community.

Blockquote Rolling cadence simply indicates that the sky coverage will not be homogeneous by season. Generally we talk about prioritizing something in “year 1” vs “year 2” etc. However, there are constraints placed on how much a region can be “front-loaded” by the science requirements of the WFD survey.

Blockquote Rolling cadence means a higher revisit cadence in a particular area of sky, but usually also means that multiple filters are done on the same field in the same night. The current OpSim implementations of a “rolling cadence” are to deprioritize an area of sky (bands in declination have been adopted as a simple example), which then either gets 0% or 25% of the baseline number of visits, and the prioritized region gets more frequent visits (not on the same night, usually the inter-night revisits stay the same).

Caution: the final implementation of rolling cadence, if used, remains to be decided.

[TomLoredo]

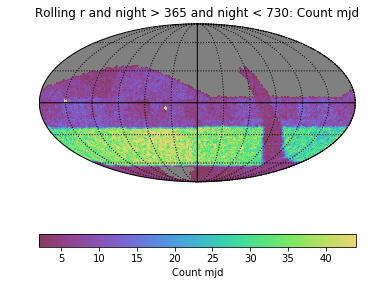
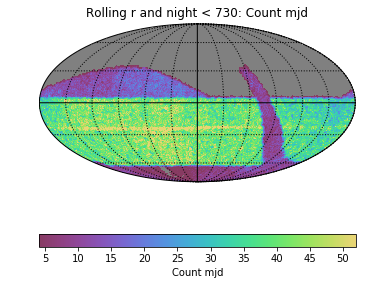
Hi Rachel et al.-

I’m far from an expert on this, but when the WP call came out, I did some digging to educate myself, and here are some early descriptions/definitions of rolling cadence.

There was an NOAO/LSST cadence workshop in 2014: LSST Observing Cadences Workshop. On the workshop web site is a lengthy report that appears to document the emergence of the idea.

The working assumption for the LSST has been a universal cadence in a WFD (wide-fastdeep) main survey, in which all fields are observed with a similar cadence and pattern. A natural extension to this universal pattern is the “rolling cadence” where the region surveyed shifts as a function of time (Recent Cadence Experiments, in this report). This provides a denser time sampling for each region on the sky for part of the survey duration, at the cost less dense sampling during the rest of the survey. [p 6]

A subsection (7.8) is devoted to rolling cadences. It describes them as follows:

Rolling cadences allow different time sampling over limited area and over limited time. They are motivated by trying to yield better SN light curves, variable star light curves and transient sampling. [p 23]

The topic is also covered in the 2017 (but, I believe, “living”) arXiv report on LSST observing strategies: [1708.04058] Science-Driven Optimization of the LSST Observing Strategy. Section 25 (by Stephen Ridgway) is devoted to rolling cadences. It begins as follows:

With a total of ~800 visits spaced approximately uniformly over 10 years, and distributed among 6 filters, it is not clear that LSST can offer the sufficiently dense sampling in time for study of transients with typical durations less than or ~1 week. This is particularly a concern for key science requiring well-sampled SNIa light curves. “Rolling” cadences stand out as a general solution that can potentially enhance sampling rates by 2× or more, on some of the sky all of the time and all of the sky some of the time, while maintaining a sufficient uniformity for survey objectives that require it.

Several pages are devoted to describing rolling cadence options and constraints. There’s a nice, short sub-subsection, 2.5.2, on “Rolling Cadence Basics”:

Assume a fixed number of observing epochs for each point on the sky, nominally distributed uniformly over the 10-year survey duration. A subset of these can be reallocated to provide improved sampling of a given sky region in a given time interval. This will have the inevitable effects of: (1) reducing the number of epochs available for that sky region during the rest of the survey (affecting, for example, proper motion studies), and (2) displace observations of other sky regions during the time of the improved temporal sampling (affecting, for example, early large scale structure studies needing high depth uniformity). In short, the cadence outside the enhanced interval will be degraded.

The essential parameters of rolling cadence are: (1) the number of samples taken from the uniform cadence, and (2) the enhancement factor for the observing rate.

For more details, it points to an LSST Project document that I haven’t yet read in detail, "A Rolling Cadence Strategy for the Operations Simulator, " by Kem Cook & Stephen Ridgway: OpSim Rolling Cadence Stratgey-ver1.3. That might be the definitive early document; it’s from April 2014, predating the NOAO/LSST workshop. It includes a 1-line definition:

Rolling cadence – a visit sequence that is applied to each part of the sky, but for only part of the survey

It then goes on to describe motivations and constraints, and to provide several rolling cadence options. It appears that, at that time, the term was used for a strategy that would be applied across the whole sky. My understanding is that the term is now used more generally. The term makes a bit more sense to me when considered as applying to the whole sky, in the sense that periods of dense and sparse coverage roll across the whole sky.

If there is ever a definitive definition, it should probably be added to the LSST Corp Astro Glossary: Astro Glossary - LSST Software User Guide - Confluence. It currently defines “cadence”:

Cadence: The sequence of pointings, visit exposures, and exposure durations performed over the course of a survey.

But it does not have an entry for “rolling cadence.” My own capsule summary might combine material from a few of the above quotes:

Rolling cadences adjust the time sampling over specified areas, reallocating samples that would nominally be distributed approximately uniformly over the survey duration so that the sampling is denser in some periods and sparser in others. Periods of dense sampling must move (roll) over the sky. Rolling cadences are motivated by trying to yield better sampling of classes of variable and transient objects. Key parameters of a rolling cadence include: (1) the areas affected; (2) the number of samples taken from the uniform cadence; and (3) the enhancement factor for the observing rate. The latter parameters may be filter-dependent.

But every time I read that I want to change something!

-Tom

[rbiswas (Rahul Biswas)]

@TomLoredo

I have found it useful to explain this in terms of static science sky area and number of visits, transient science sky area and cadence during windows of time << survey duration.
In that sense the aimed effect of rolling cadence is to keep the static science area and number of visits constant while improving the cadence for transient science over periods of time << survey duration at the cost of reducing transient science area.

Slightly off-topic, this is an unfortunate term, but we are probably stuck with it. It is highly confusing due to the existence of a similar term in supernova studies ‘rolling search’ which simply means un-targeted scanning over the survey area, that it has little to do with.

[TomLoredo]

@rbiswas: I like this:

the aimed effect of rolling cadence is to keep the static science area and number of visits constant while improving the cadence for transient science over periods of time << survey duration at the cost of reducing transient science area.

I might alter it slightly: at the cost of reducing transient science area*time (or perhaps “exposure,” though not quite in the usual sense), or maybe ~instantaneous area. In principle, the area with enhanced sample rate could be the whole sky, just not all the time. That seems to have been the original idea, with “rolling” referring to how periods of increased sample rate might roll across the whole sky.

[rstreet (Rachel Street)]

Many thanks, @TomLoredo and @rbiswas for your replies, this is very helpful.

[yoachim (Peter Yoachim)]

OK, people wrote a lot of good words, but I think rolling cadence is a lot easier to understand with plots.

Here’s a baseline-like simulation, number of observations take in r-band in year 1, year 2, and then combined.

In these, year 1 looks a lot like year 2.

Now for a rolling cadence simulation:

In these, the WFD area has been split in half, and in year 1 the north gets more emphasis, and in year 2 the south. At the end of two years, the sum looks very similar to the baseline simulation (there’s an extra stripe on the border, that happens because of having a sharp border but still dithering).

For static science, the end of year 2 looks about the same in both sims. For transients, the rolling cadence has potential to return much better sampled light curves (on the part of the sky that has extra emphasis). Note the color bars are on different scales.

We get the term “rolling cadence” because we designate an area to have an increased cadence (and because there’s no free lunch, also an area with deceased cadence) and then “roll” those areas around the sky so that at the end of the survey the sky is fairly uniform. We could increase the cadence on 1/3 of the sky and decrease on 2/3 of the sky, then have an even survey every 3 years.

The more aggressive would be to only image 1/10th of WFD each year. Then we risk getting artifacts with a year of bad weather, or aliasing with solar system objects, but light curves would be really well sampled!

[rstreet (Rachel Street)]

@yoachim These pictures are indeed worth a thousand words, many thanks for this explanation.